フィボナッチ数列は、一般に、「前々項前項=自項」となる数列ですので、 (1)前々項と前項 (2)前々項と自項 (3)前項と自項 の三つのうちどれか一つの組み合わせが判れば、三数のうちの残りの数値を求める事がで きます。May 31, · これがプログラミング入門としてフィボナッチ数列を扱う際の最もオーソドックスな解法でしょう。 私たちが「n番目のフィボナッチ数列を求めて」と言われて暗算する時も大抵はこの方法を使うと思います。 Python3では以下のように書くことができます1 1 2 1 3 2 4 3 5 5 6 8 7 13 8 21 9 34 10 55 11 12 144 13 233 14 377 15 610 16 987 17 1597 18 2584 19 4181 6765 21 22 23 24 25 26 27 28 29 30 40 31 32 33 34 35 36 37 38

黄金比 モデュロール フィボナッチ数列 Archicad For Beginners
フィボナッチ数列 階段
フィボナッチ数列 階段-Mar 11, 12 · フィボナッチ数列について質問です 「10段の階段を1段または2段ずつ登るとき、登り方は何通りあるか?」という問題なんですがこの回答がフィボナッチになる理由がイマイチよくわかりません。どなたか解説をお願いします。 フィボナッチ数列は漸化式を用いるとFn2=Fn1Fnで表されますフィボナッチ数列に感動 階段を1段ずつもしくは2段ずつ(つまり、一段飛ばしで)上っていくことを考える。 (1)3段の階段を上る方法は何通りあるか。 (2)15段の階段を上る方法は何通りあるか。 答えは後ほど。 金曜日の講義で数列の話が出てきました




灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン
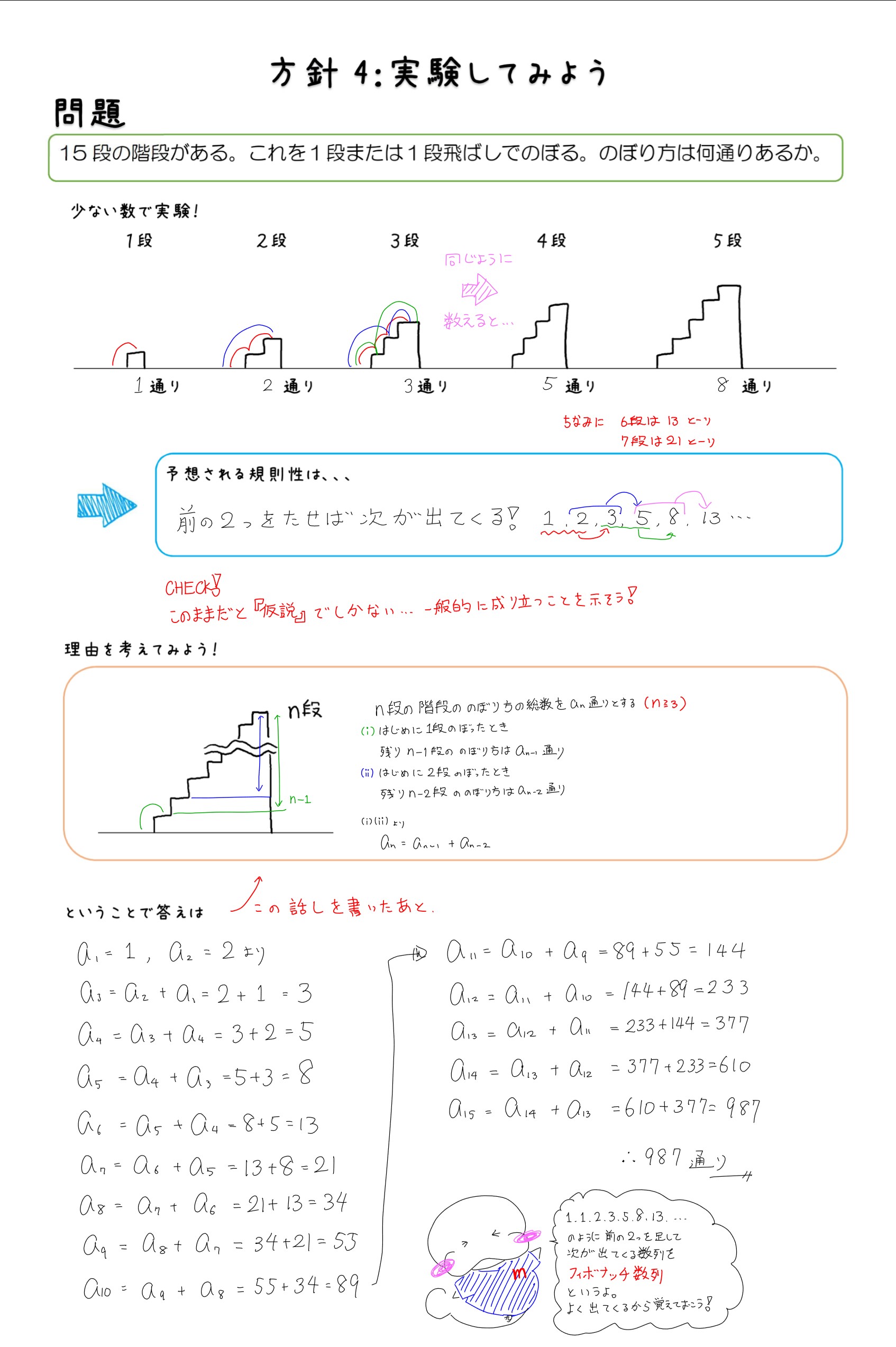
フィボナチ数列 13 5 Written by ma{ (caLabo) 1 階段上りの問題 ある人が, 15 段ある階段を上ろうと思います。 上り方は「次の段に上る」か 「1 段飛ばして上る」の2 通りをその都度選べるものとすると, ちょうど15 段 を上り切るまでの登り方は何通りあるか。Mar 26, 21 · n 段の階段を1段または2段ずつ上るときに、上る方法の数を F n1 通りとすると、F n はフィボナッチ数列となる。 これは数学的帰納法で証明できる。 n=1 の時は、1段上りの1通りしかないのでF 2 =1で正しい。 n=2 の時は、1段上りと2段上りの2通りがあるので、F 3 =2で正しい。Mar 26, 19 · 従来、このきまり(フィボナッチ数列)で階段の登り方の場合の数を求めてきたのですが、先生も児童も、本当に34通りあるのか、書き出したことがなく、また、なぜフィボナッチ数列になるのか理由を考えたことがありませんでした。
May 22, 16 · 意外や意外、音楽の世界もフィボナッチ数列にしっかり支配されているのでした。これまでにエジプトのピラミッドだとか、モナリザの絵の中に見出される黄金比などとの関係は盛んに議論されて来ましたが、音楽の世界もフィボナッチ数列で支配されているとは聞いたことがありませMar 25, · つまり、1段2段の上り方のある階段問題は 2つ前か1つ前からしか上がってこれない仕組みとなっている ため、 階段の上がり方はフィボナッチ数列 になります。 まとめ ・階段問題(1,2段)はフィボナッチ ・1つ前、2つ前から来る問題はフィボナッチApr 09, 21 · 階段上りとフィボナッチ数列と場合分け中学受験プロ講師ブログ(閲覧日:21年4月11日) フィボナッチ数列の性質6 すぐる学習会 (閲覧日:21年4月11日)
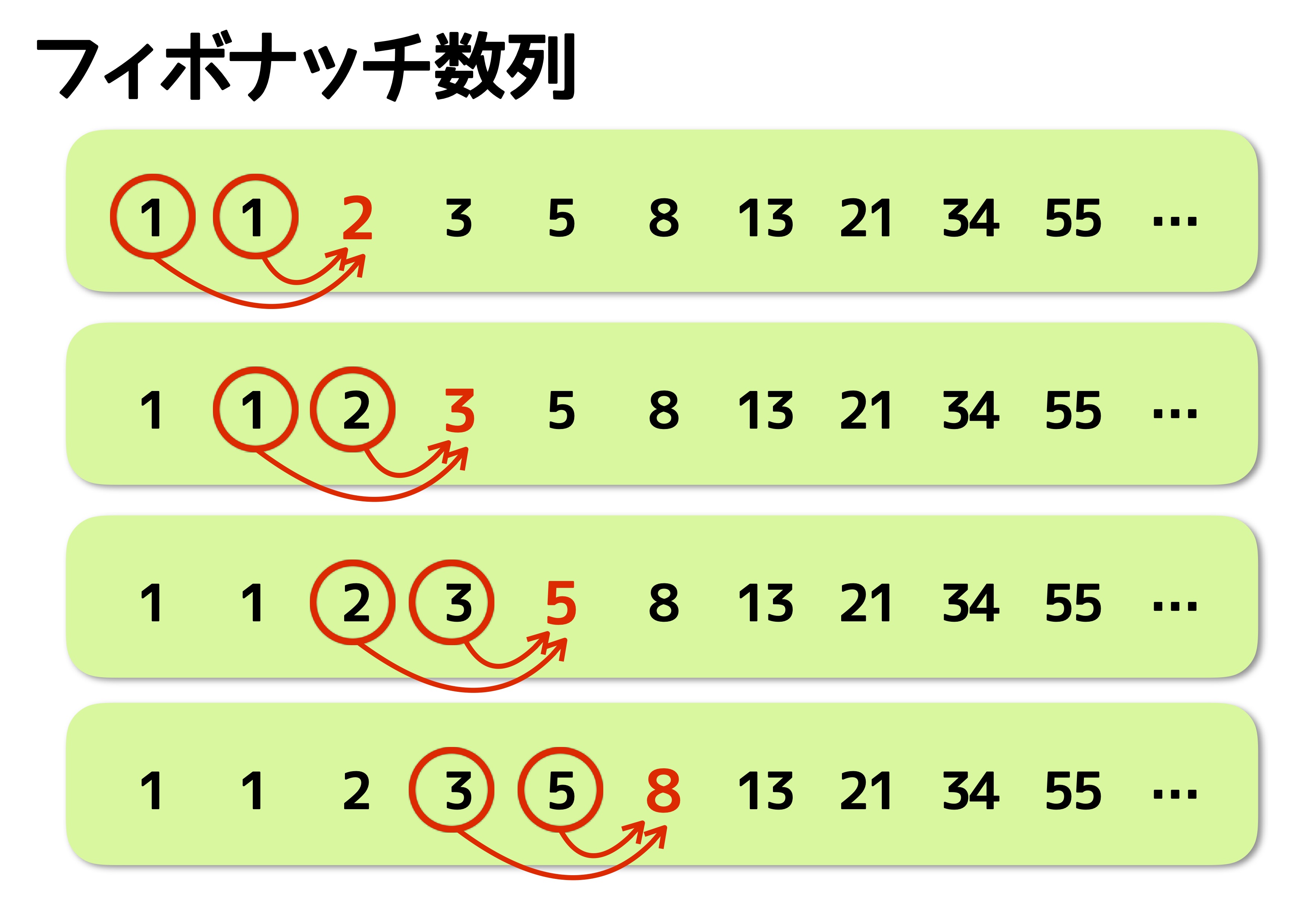
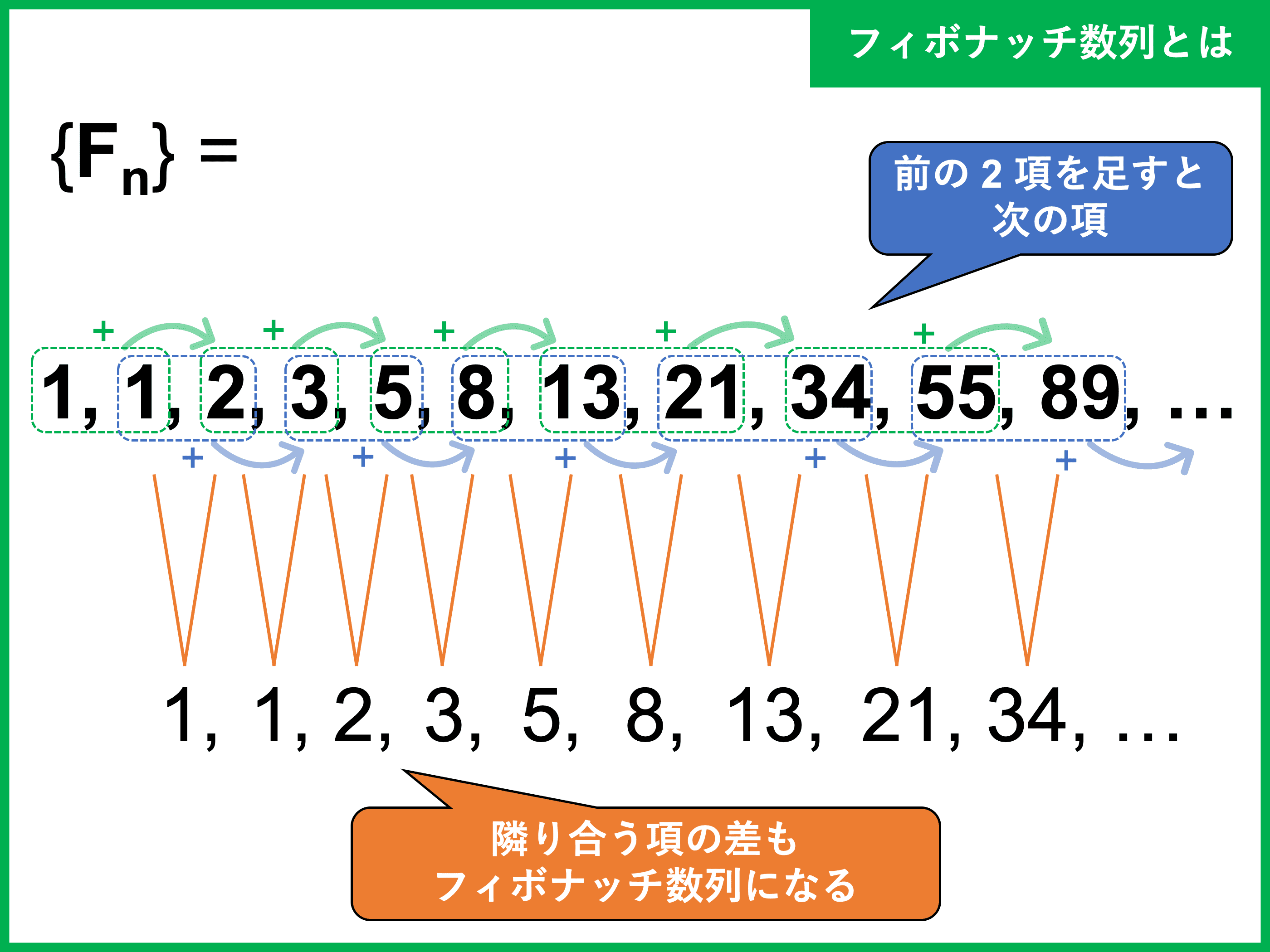
Jan 26, 18 · フィボナッチ数列とは フィボナッチ数列とは、「1番目と2番目の数値は 1であり、3番目以降の数値は直前の2数の和である数列」のことです。 言葉ではイメージできないものの、具体的に書くと以下のような数列になります。 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144Feb 19, 21 · フィボナッチ数列の中から \(2\) つの数を取り出したとき、その \(2\) 数の最大公約数もフィボナッチ数列の中にある;Oct 06, 17 · フィボナッチ数列とは。 一般項の証明・黄金比との関係について フィボナッチ数列は「 隣り合う2つの数を合計すると次の数になる 数列」です。 英語では Fibonacci Sequence 名前の由来は数学者レオナルド・フィボナッチより 具体的に書き並べていくと 1, 1



場合の数 プロアンズ



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ
May 17, 19 · 階段の問題で「1段ずつ」「1段飛ばし」「2段飛ばし」の3種類が可能なら「トリボナッチ数列」になります。バスケットボールの点数の入り方も同様です。 ※前2つを足すのが「フィボナッチ数列」なら、前3つを足すのが「トリボナッチ数列」です。Sep 01, · 階段を上る方法について、一段ずつ考えて7段目まで数えてみましょう (忙しかったら数えなくてもOK)。 漏れなく数えられればこのようになるはずです。 しかし、このあたりで数えるのが厳しくなってくるはず。 本当に数え忘れが無いのか? と不安にPerformance 計算 フィボナッチ数列 階段 サブライン時間におけるn番目のフィボナッチ数 (9)




75 数列 中学 受験 最高のぬりえ




黄金比とは 基本的な考え方とデザインへの取り入れ方
May 26, 17 · まずは、フィボナッチ数列とは何かについて説明します。 数列で説明 フィボナッチ数列は、「2つ前の項と1つ前の項を足し合わせていくことでできる数列」のことです。数列は「1,1」から始まり、 1, 1, 2, 3, 5, 8, 13, 21 と続いていきます。 これを漸化式で表すと、階段の上がり方(フィボナッチ数列など) 場合の数で「階段の上がり方」という有名な問題があります。 例えば、次のような感じです。 階段を1歩につき1段か2段で上がるとき、7段の階段の上がり方は何通りありますか。 この問題は決して易しくない(初見だと解けない受験生が多い)のですが、ほとんどの受験生が解法を教わっていることと、解法を知っていれ中学受験 算数 動画解説 場合の数 階段の上り方(フィボナッチ数列・トリボナッチ数列)10 段からなる階段があり,1 段上がりと2 段上がりの




読むeラーニング 整数と周期1 小澤淳の最強の算数 Eラーニングポータルサイト Elearning Co Jp Eラーニング専門企業 株 キバンインターナショナル




ガウディの足跡10 サグラダファミリア 内部 Cafe Mare Nostrum
であるから,これはF2m(フィボナッチ数列の第2m項)になっていることがわかる. F2m=F2m1+F2m2 と順次計算することによって m/n 1 2 6 1 233 7 1 610 8 1 1597 9 1 4181 10 1等比数列rn がフィボナッチ数列を満たすと仮定して漸化式に代入するとrn2 = rn1 rn です から、両辺をrn で割ってr2 = r 1 です。 もちろんr = 0 の場合は除外しておきます。 この二次 方程式を解いて得られる 1= p 5 2, = 1 p 5 2 をr と見なして二つの等比数列がフィボナッチ数 列を満たしますからFeb 24, 18 · このようにフィボナッチ数列とは、 前の二つの数を足した数が次の数となる という性質を持っています。 黄金比に向かうフィボナッチ数列 フィボナッチ数列を語る上で欠かせないのが、黄金比との関係です。




Hamon To Rasen To Fibonacchi Suri No Megane De Miete Kuru Seimei No Katachi No Shinpi Shigeru Kondo Amazon Com Books




リュカ数列
Apr 16, 06 · 1 数列の問題で 階段の登り方の漸化式の立て方が分かりません。 問題はなんでも良いのですが、 まあ、一段 2 フィボナッチ数列です。 数列{fn}の奇数項を抜き出した数列の和を考えますMar 08, 08 · アトランタの個人邸宅に76段の民主主義的階段を作った。 全長80mである。 秩父、オハイオ、フィティアンガ(ニュージーランド)に続き、今回が4本目である。 途切れのない一連の階段としては、今までで最も長いものになった。3 フィボナッチリトレースメントを使ってfxで利益を出す3つのステップ 31 ①エリオット波動の1波が出




コーディングテスト対策 フィボナッチ数列を用いてleetcodeのclimbing Stairsをrubyで解く Youtube



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ
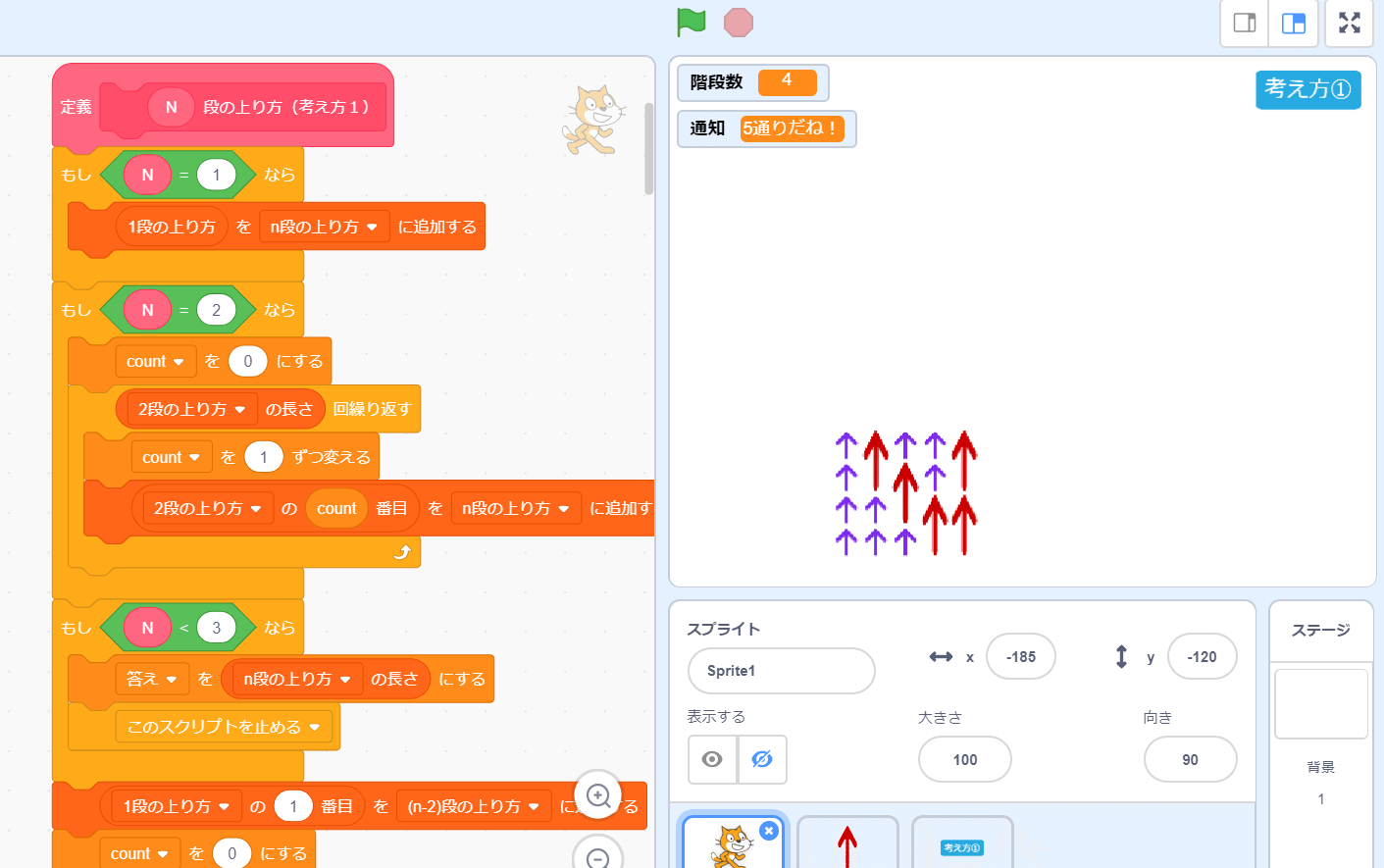
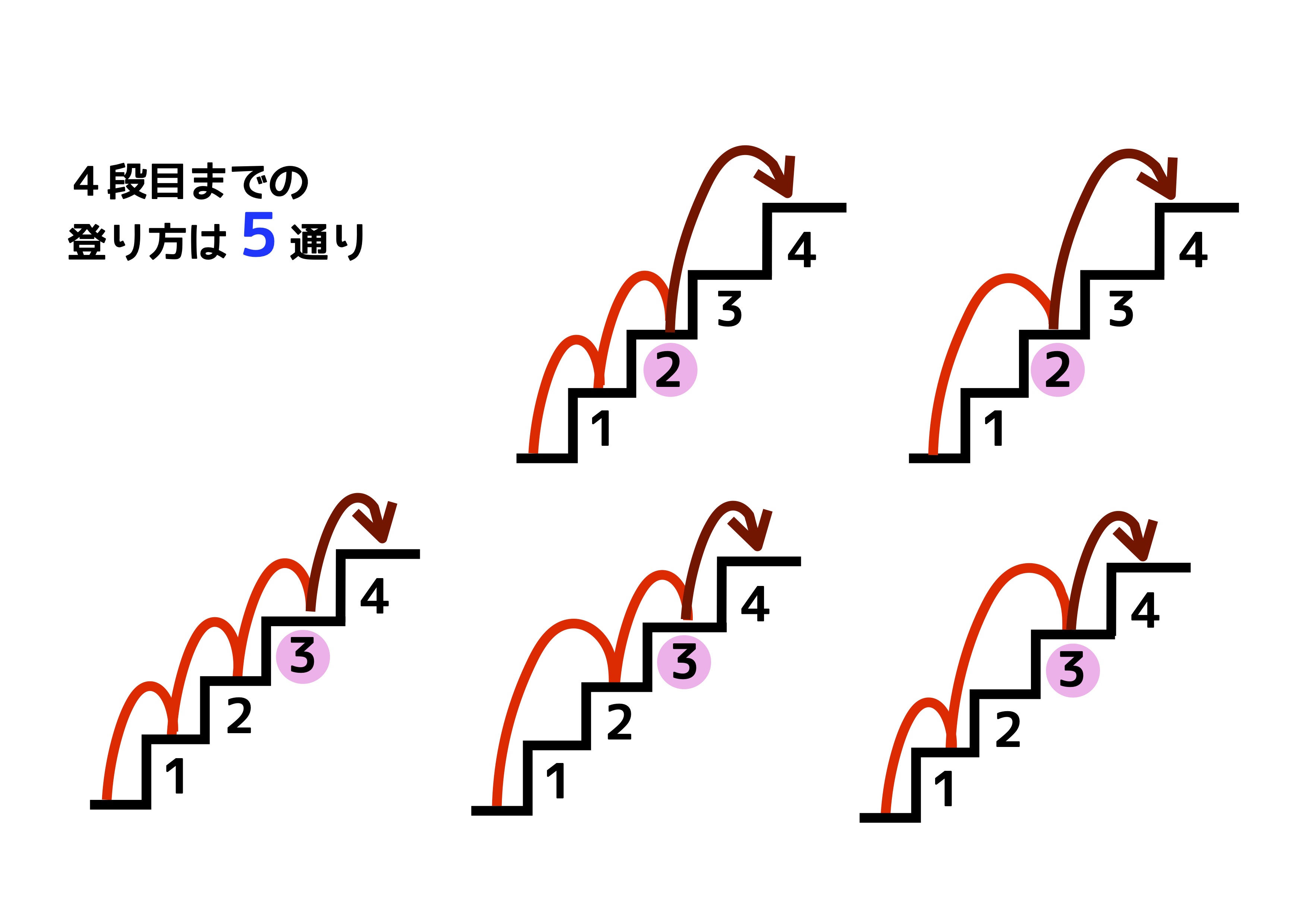
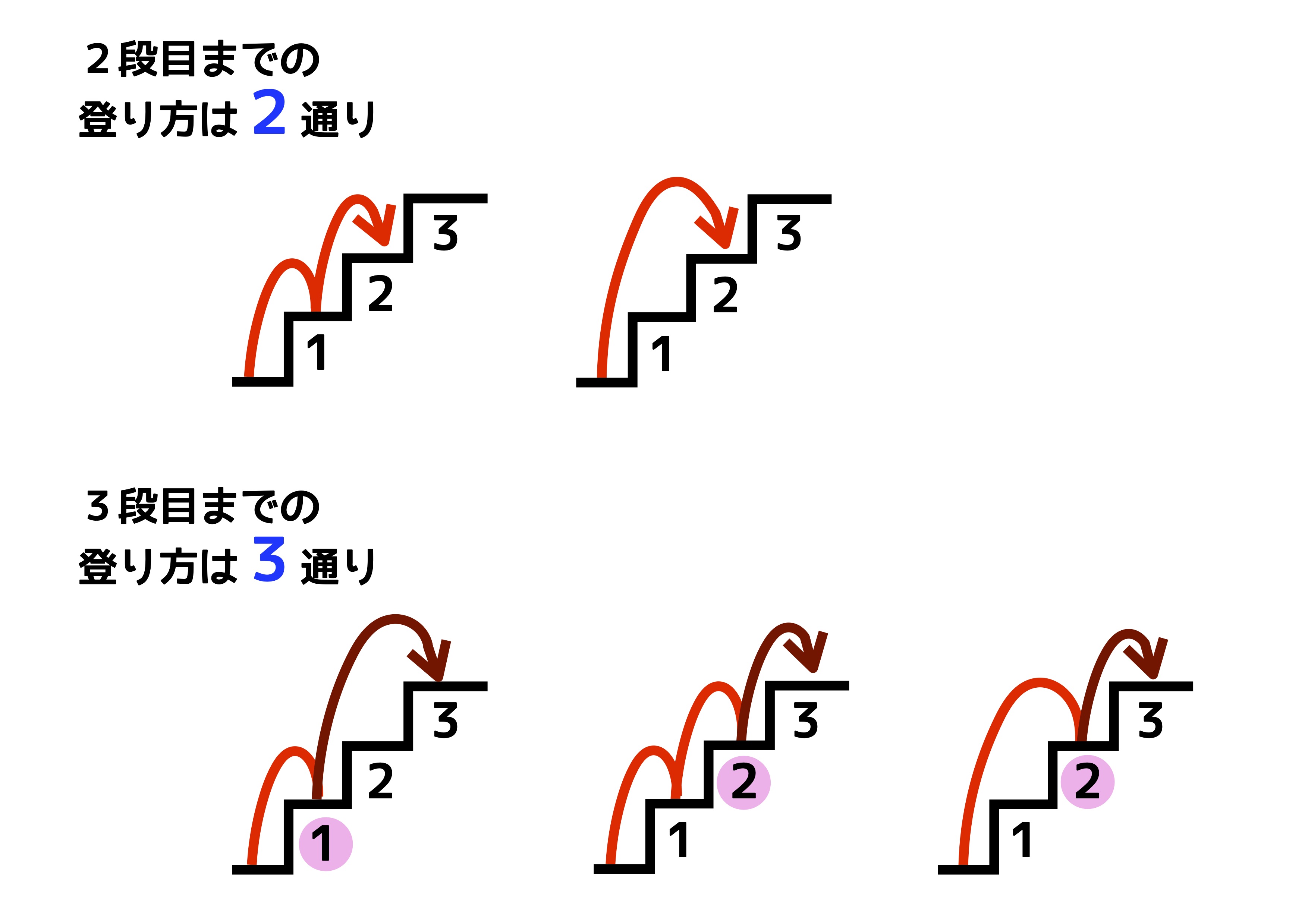
4001番目から5000番目までのフィボナッチ数列 5001番目から6000番目までのフィボナッチ数列 6001番目から7000番目までのフィボナッチ数列 7001番目から8000番目までのフィボナッチ数列 8001番目から9000番目までのフィボナッチ数列 9001番目から番目までのフィボナッチ数列 フィボナッチ数列は自然界でよく出てくる 花びらの枚数,木の枝分かれ,まつぼっくりのNov 28, 19 · フィボナッチ数列は、直前の2つの項の数を足したものが次の項の数になる数列です。そのためこのような結果になるんですね。規則自体はとてもシンプルです。一度でもフィボナッチ数列を見たことがあれば、規則性はすぐに理解できるでしょう。Nov 23, · 考え方はフィボナッチ数列とまったく同じです。ただし、フィボナッチ数列は最初の2項が「1,1」であるのに対し、階段問題では「1,2」で始まることにご注意ください。 ですから、 🌻n 段の階段を1段または2段ずつ昇るときに、昇る場合の数は Fn1 通りある
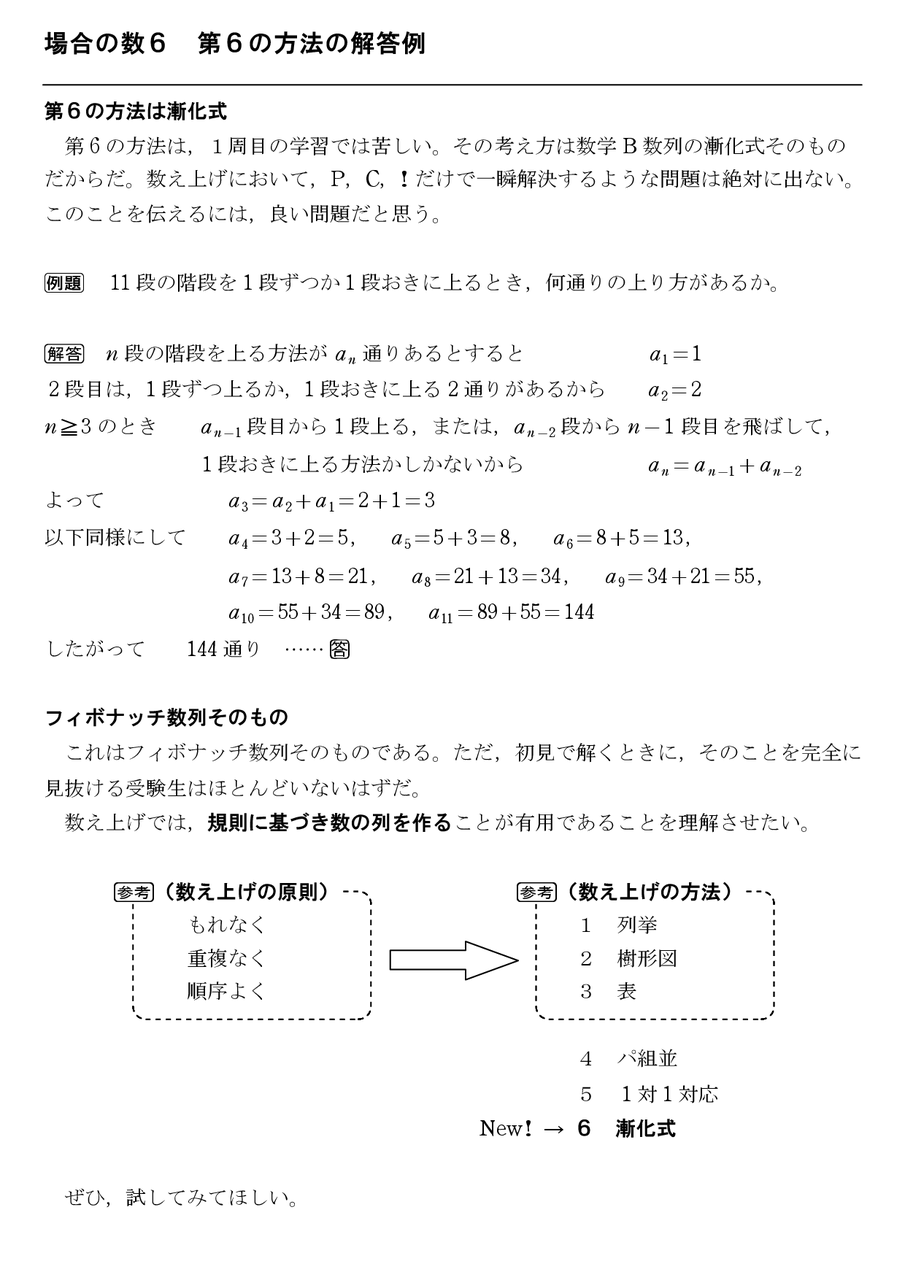



場合の数6 第6の方法の解答例 怜悧玲瓏 高校数学を天空から俯瞰する



フィボナッチ数列 Of 京極一樹の数学塾会員頁
Jun 11, 19 · フィボナッチ数列というのは、 1、1、2、3、5、8、13、21、34、55、 というように、前の2つの数の和が次の数になる数列です。 先ほどの問題のような、「1歩で1段or 2段」で階段を上がる方法というのは、フィボナッチ数列とは 1,1,2,3,5,8,13,21,34,55, という数列は, ・最初の2つが1で ・3つめ以降は「前の2つを足した値」になっています。 例えば, 5 8 = 13 58=13 5 8 = 13 なので, 5, 8, 13 5,8,13 5, 8, 13 が並んでいます。このような数列のことをフィボナッチ数列と言います。階段アルゴリズムの応用 みんなから「それはフィボナッチ数列だ」と言われてしまいました。 しかし、階段アルゴリズムはフィボナッチ数列だけではありません。 階段の例であっても、一度に3段、4段、それ以上登れるという問題も考えられます。 また




場合の数 階段を昇る昇り方は何通り 恋する中学受験 大学受験を見据えた中学受験




多肉植物の投稿画像 By しらたまさん フィボナッチ数列と植中毒とエケベリア属と多肉女子とレオナルドダビンチとペインテッドレディ と興味津々とかわいいな 19月2月11日 Greensnap グリーンスナップ
Nov 30, 14 · 1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるか。07 京都大・理乙イズミの解答への道有名な問題の亜流。漸化式を立てて、数えていくのが鉄則です。2段をNov 29, 14 · それは「最後に登るのが何段か」、いいかえれば「何段手前から登ってきたか」に着目するということです。 どのような場合でも最後の登り方は1段か2段です。 3段目にたどりつくには、1段目から登るかか、2段目から登るかのどちらかしかないということです。 さきほどの例でいえば、 (1段 – 1段) 1段 (2段) – 1段 1段 – 2段 のように見て、( )の部分はMay 21, 21 · 目次 1 フィボナッチリトレースメントとは 11 ①フィボナッチ数列とは;




フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ




螺旋階段 模型 簡単 Imsmedia Org
数学では、フィボナッチ数は以下の数列です: 定義上、最初の2つのフィボナッチ数は0と1であり、残りの数は前の2つの合計です。 いくつかのソースは、2つの1でシーケンスを開始する代わりに、最初の0を省略します 。May 02, 10 · フィボナッチ数列の質問です。「N段の階段を1段ずつか2段ずつ(1段とばし)で上るには何通りの上り方があるか」これはフィボナッチ数列になるとのことですが、腑に落ちません。()内の'1段とばし"に意味が あるのでしょうか?ポイントのような気がします。小学生にもわかるよ(2) あなたは黄金比の魔法を使うことができます:φ=(sqrt(5)1)/ 2とし、 fib(n) =(φn(1φ) n )/ sqrt(5)を定義します。 そのような関数を明らかな方法で怠惰なリストに変換することができます:Haskellでは以下のように動作し




黄金比 モデュロール フィボナッチ数列 Archicad For Beginners




小6算数 場合の数 階段の登り方 ベネッセのプログラミング教育情報
1段または2段づつ移動可能な7段のぼりの場合の数は 「オンボロ階段」などで解説されているように「フィボナッチ数列」で表すことができます。 即ち F n =F n1 F n2 F 0 =1,F 1 =1 より F 7 =21です。フィボナッチ数列 階段 (6) フィボナッチ数は、コンピュータサイエンスの学生のための再帰の一般的な導入となっており、自然の中で存続するという強い主張があります。これらの理由から、私たちの多くはそれらに精通しています。
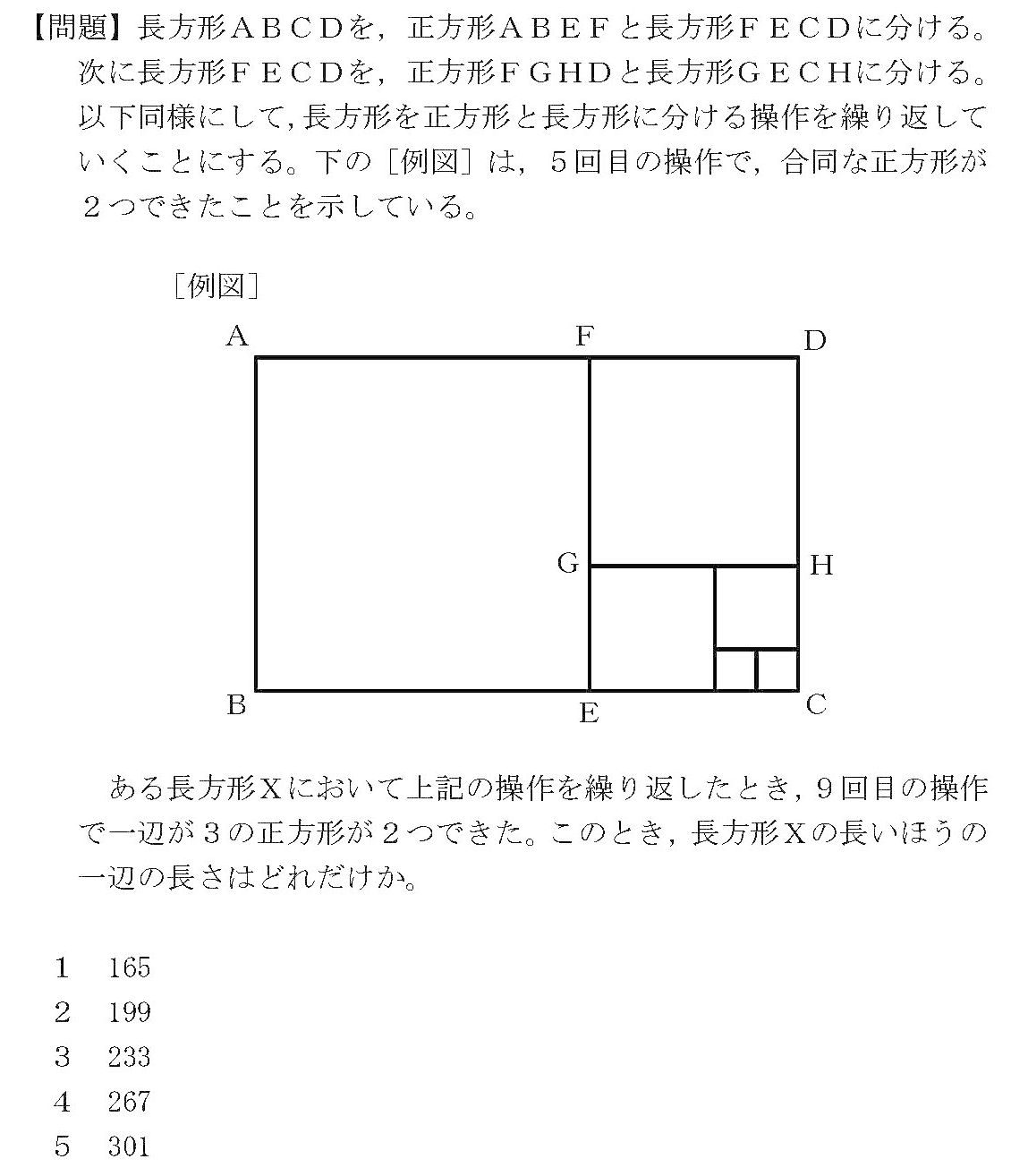



裁判所19 フィボナッチ数列 岡野朋一 Note




一瞬でフィボナッチ数の無限和が 1であることを示す Youtube




螺旋階段 模型 簡単 Imsmedia Org




眠れなくなるほど面白い 図解 数列の話 松下 哲 本 通販 Amazon




全てはゼーレのシナリオ通り 猫の醸し出すポーズはフィボナッチ数列に裏打ちされていた カラパイア




De Gulden Snede おしゃれまとめの人気アイデア Pinterest Eotgyb 幾何学図 フィボナッチ ハンドレタリングアート




001 フィボナッチ数列 コマ大数学科 Qiita




フィボナッチな日常 ひまわりの種から黄金比まで コペルくんwithアヤ先生 Note大学初代教授 Note
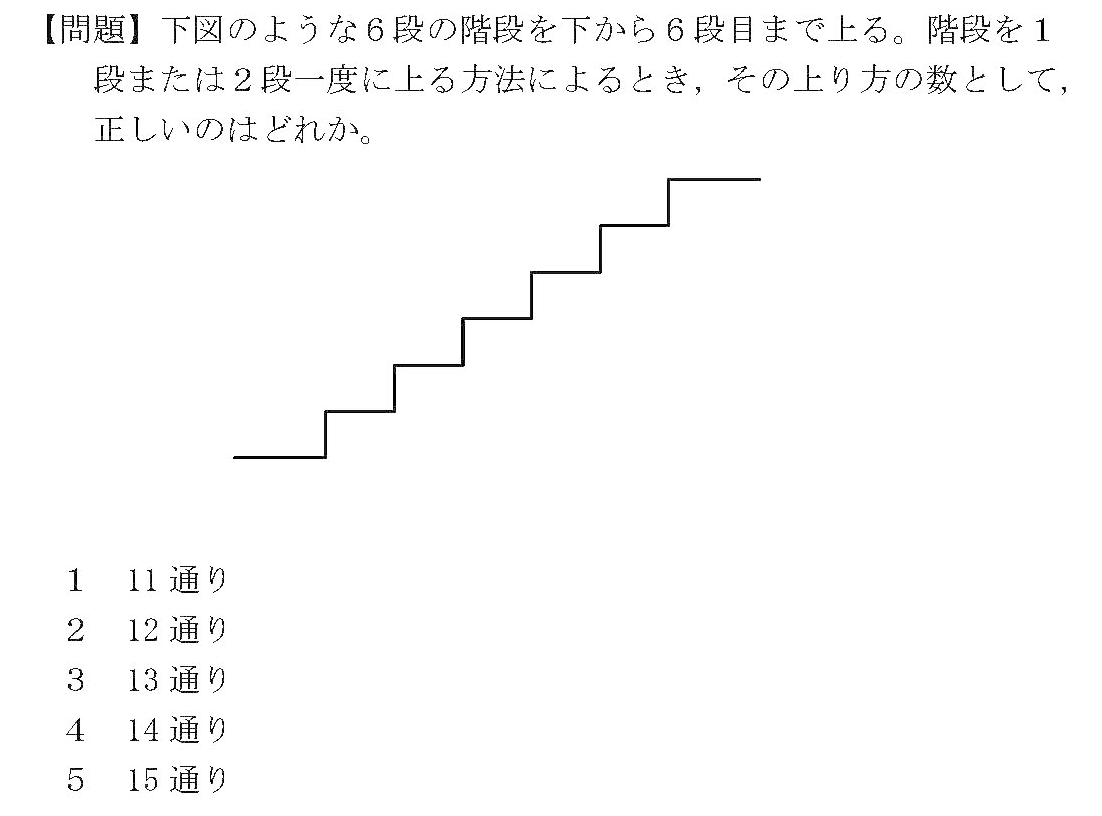



警視庁16 フィボナッチ数列 岡野朋一 Note




111 フィボナッチ数列は2進数でも美しいのか 15歳少女が研究 内容を評価され受賞 141




薄紅色の螺旋階段 街並み 建物 その他 Ganref




螺旋階段のカード 星名恵光 ほしなめぐみ のブログ
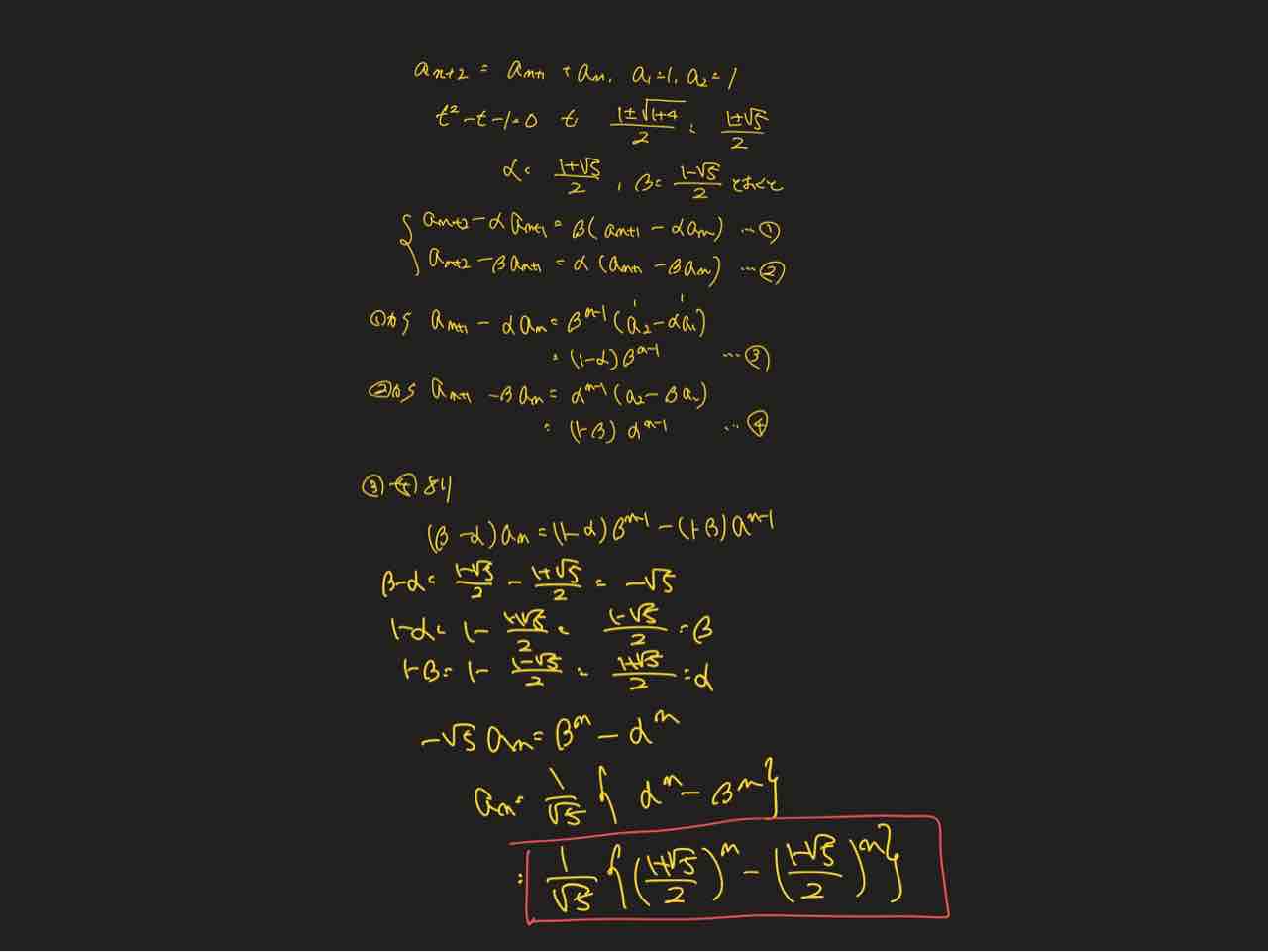



数学b フィボナッチ数列の絵本と階段 学習村の 国公立へ行こう




ひまわりに隠されたフィボナッチ数列と黄金比 ひまわりは黄金の花 数学の面白いこと 役に立つことをまとめたサイト ひまわり フィボナッチ数列 フィボナッチ




ゆな 動的計画法 道順の書き込み式による求め方 階段登りの場合の数を求める漸化式 書き込み式 フィボナッチ数列と黄金比 場合の数 漸化式 数列 フィボナッチ フィボナッチ数列 黄金比 極限 性質証明




数学b フィボナッチ数列の絵本と階段 学習村の 国公立へ行こう




デザインの中に隠された黄金比の秘密を探る Wokobo



Pythonによるフィボナッチ数列の色々な求め方 一般項 反復法 再帰法 Qiita




波紋と螺旋とフィボナッチ 角川ソフィア文庫 近藤 滋 本 通販 Amazon




75 数列 中学 受験 最高のぬりえ
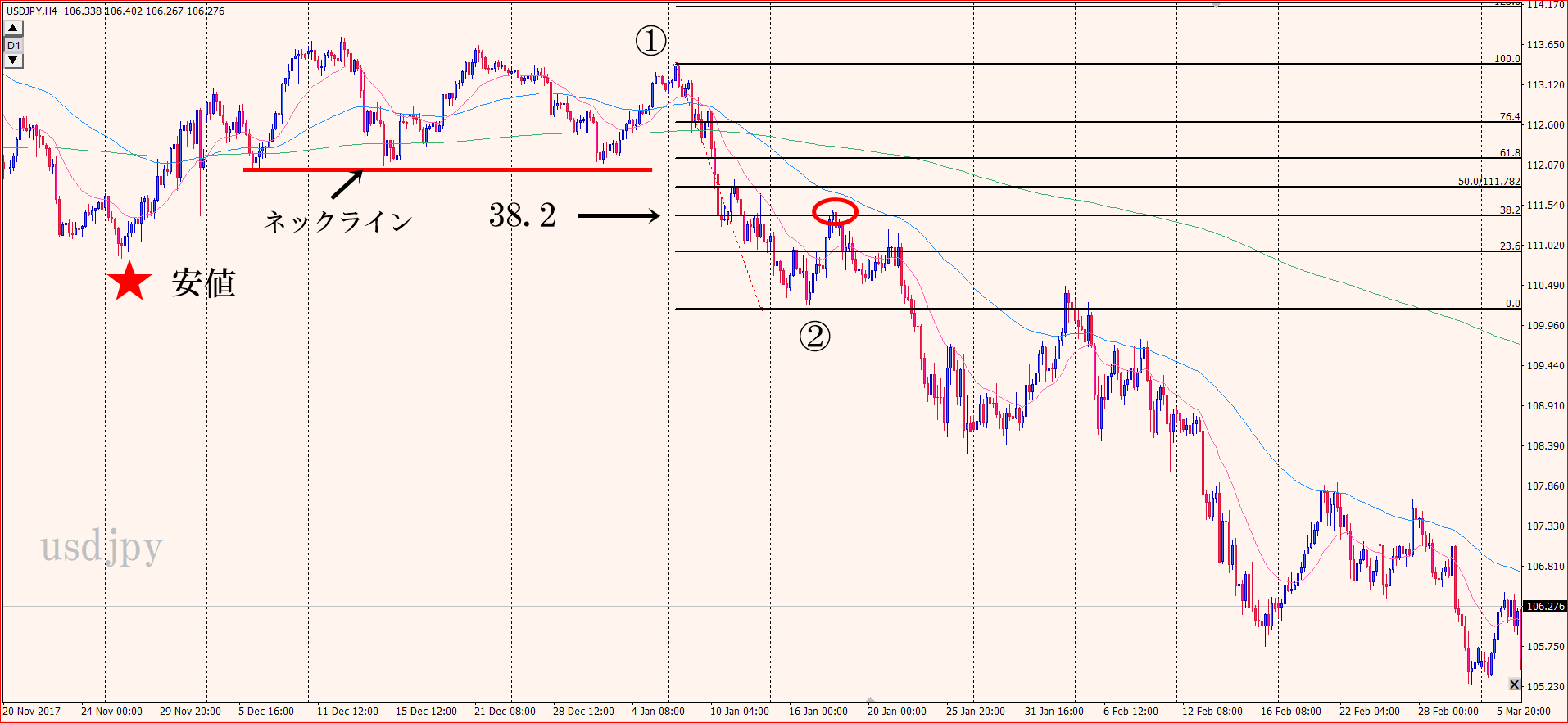



フィボナッチリトレースメントを使ってfxで利益を出す3つのステップ アラフィフゆんのfx宅トレ講座




フィボナッチ数列と美の関係 ヘアスタイルにも当てはまる 小原昇隼 氏 Devonshire Hairstudio 金田健 氏 Sherpath代表 教育対談 Singalife 在シンガポール日本人向けのフリーマガジン グルメ 習い事 ビジネス 教育など充実の内容満載のウェブサイト



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ




フィボナッチ数列 9 Youtube




フィボナッチ数列 Hear
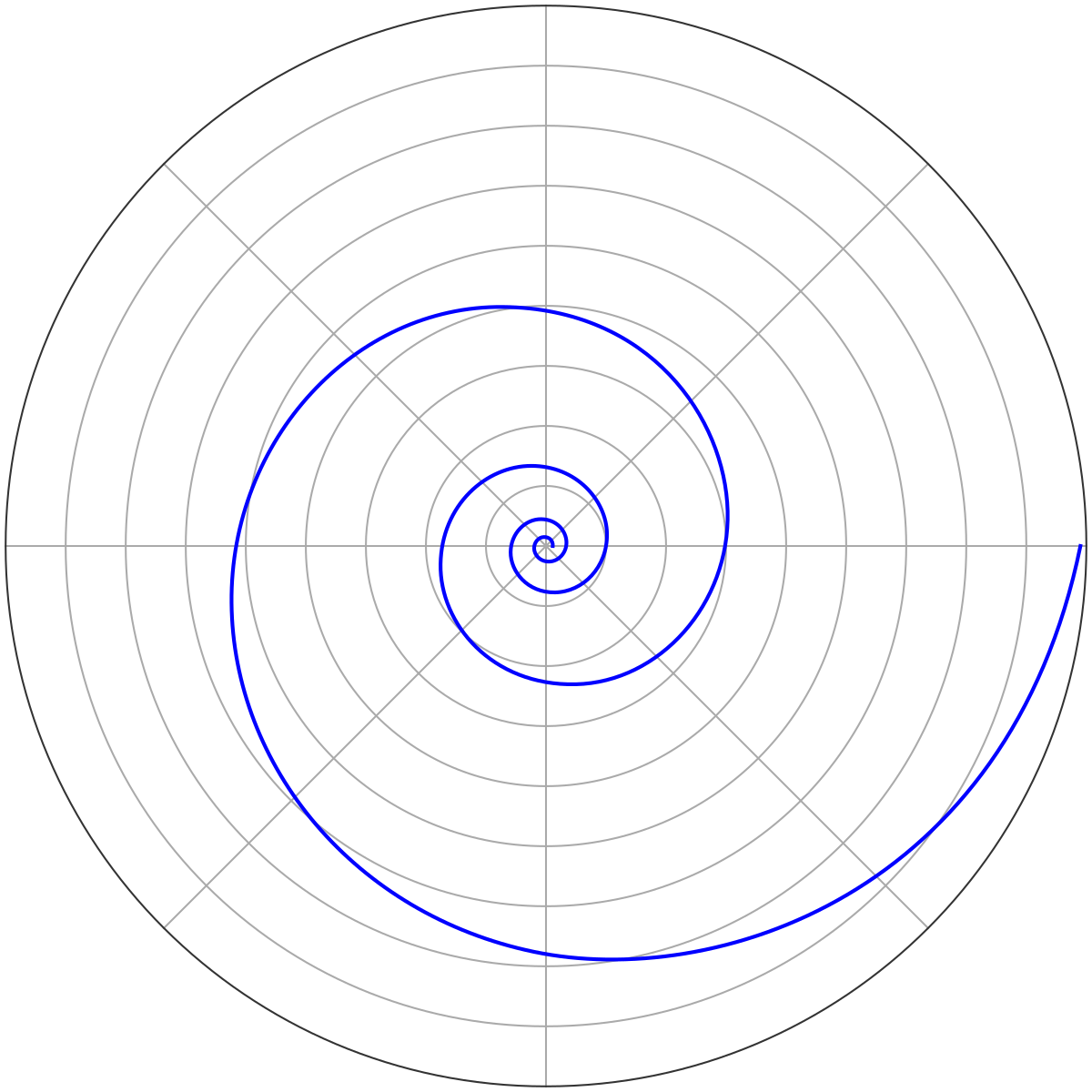



対数螺旋 Wikipedia




中学受験算数 難問 階段の上り方 フィボナッチ数列って知ってる 毎日1題中学受験算数38 Youtube




フィボナッチ数列について その3 フィボナッチ数列はどこで使用され どんな場面に現れてくるのか 自然界以外 ニッセイ基礎研究所




予習シリーズ 6年生上 第5回 理解を深めよう Youtube



Fibonacci Pavilion



昨日の高2数学 Aの追加問題が届いています ワークショップ塾長 石井里沙のつぶやき




数列 Twitter Search




ゆな 動的計画法 道順の書き込み式による求め方 階段登りの場合の数を求める漸化式 書き込み式 フィボナッチ数列と黄金比 場合の数 漸化式 数列 フィボナッチ フィボナッチ数列 黄金比 極限 性質証明



フィボナッチ数列 数学入試問題



リュカ数列




波紋と螺旋とフィボナッチ 近藤 滋 本 通販 Amazon




灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン




黄金比 モデュロール フィボナッチ数列 Archicad For Beginners




数列 Twitter Search




75 数列 中学 受験 最高のぬりえ




ガウディの足跡10 サグラダファミリア 内部 Cafe Mare Nostrum



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ




数列 英文




フィボナッチ数列の問題をケーリーハミルトンの定理と数列で解いてみたんですが 間違った Clear




Mathematics And Other Details 人生 数学 そして美しさ 永遠のそして溶けない協会



1 2 Lihat Cara Penyelesaian Di Qanda




階段の象徴的なライト F邸 その他事例 Suvaco スバコ



Fx フィボナッチボリンジャーバンドはフィボナッチatrバンドと呼んだほうが良い




一瞬でフィボナッチ数の無限和が 1であることを示す Youtube




数列 Twitter Search




数学b フィボナッチ数列の絵本と階段 学習村の 国公立へ行こう




フィボナッチ 世界ブログ



フィボナッチ数列について その3 フィボナッチ数列はどこで使用され どんな場面に現れてくるのか 自然界以外 ニッセイ基礎研究所



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ




フィボナッチ数列の問題をケーリーハミルトンの定理と数列で解いてみたんですが 間違った Clear




Withe通信 フィボナッチ数列と黄金比と美 Withe 広大生学習支援団体 Note




75 数列 中学 受験 最高のぬりえ




灘 開成の入試に頻出 図形に潜む フィボナッチ数列 の問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン




名大附過去問挑戦 算数 その2 名大附中に合格しよう Note




開成番長 算数4 フィボナッチ数列 Youtube




1 マヤの7つのチャクラ遺跡 はフィボナッチ数列に並んでいた Misaのブログ




イメージde暗記ポイント 147 フィボナッチ数列 中学受験ドクターはプロ講師の個別指導塾 家庭教師




古い家にあるらせん階段 フィボナッチ スパイラル の写真素材 画像素材 Image




前回のポイント 写像の合成 積 結合的 ℎ Ppt Download




情報数学 第6回 帰納法 資料の4 教科書4章後半 Ppt Download



Images Of レオナルド フィボナッチ Japaneseclass Jp



みんなの算数オンライン 中学受験 5年 場合の数2 モンモールとフィボナッチ 例題と解説



住んでみないと分からないワタマンのメリット デメリット みやままひろ Note
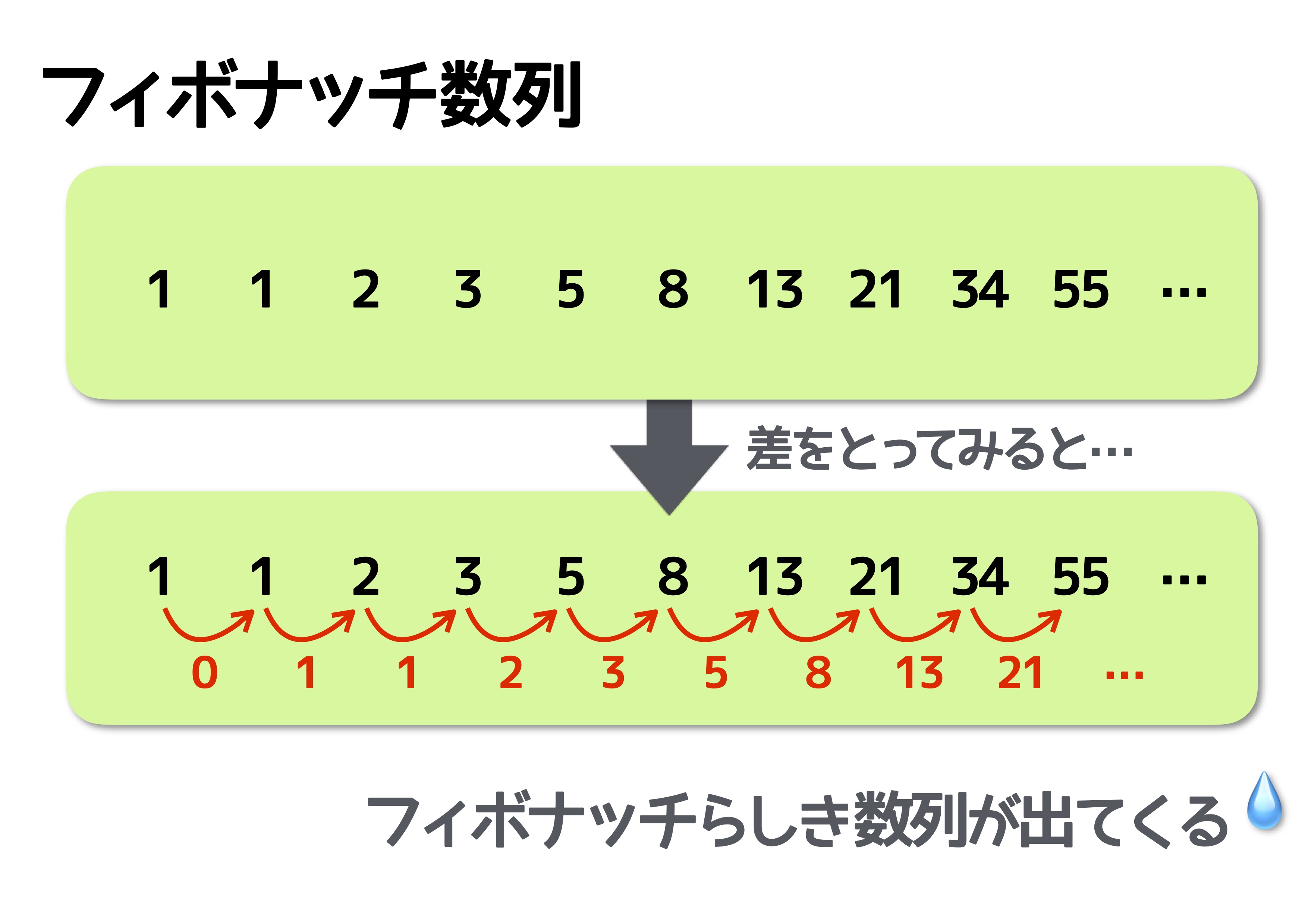



フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ




Wzrhnpcyoq3uem



0 件のコメント:
コメントを投稿